

任务:根据前几年的投产数据,预测当年每月可能的投产次数,绘制曲线图
环境:python3
工具:jupter
首先引入容器中已有的库:
1 | from sklearn.linear_model import LinearRegression |
pymysql 没有,需要安装。
如能访问外网安装方式:
!pip install pymysql -i https://pypi.mirrors.ustc.edu.cn/simple/
使用内部源在线安装pymysql:
1 | !mkdir ~/.pip/ |
提取训练数据:
1 | PREYEAR = 2021 |
1 | #变更数据类型 |
1 | # 开始线性回归 |
Out:

1 | ### 分组处理开始 |
Out:
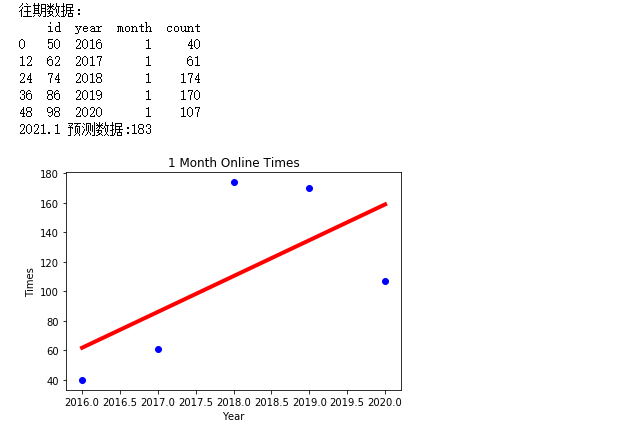
1 | df_result.head(50) |
Out:
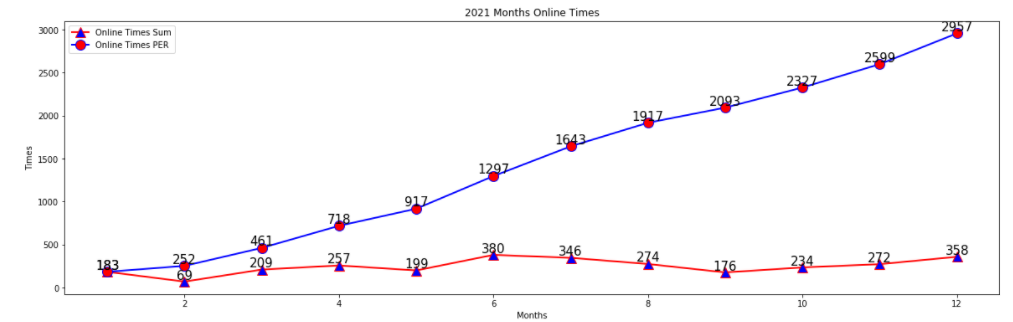
| id | year | month | count | sumCount | |
|---|---|---|---|---|---|
| 0 | 0 | 2021 | 1 | 183 | 183 |
| 1 | 1 | 2021 | 2 | 69 | 252 |
| 2 | 2 | 2021 | 3 | 209 | 461 |
| 3 | 3 | 2021 | 4 | 257 | 718 |
| 4 | 4 | 2021 | 5 | 199 | 917 |
| 5 | 5 | 2021 | 6 | 380 | 1297 |
| 6 | 6 | 2021 | 7 | 346 | 1643 |
| 7 | 7 | 2021 | 8 | 274 | 1917 |
| 8 | 8 | 2021 | 9 | 176 | 2093 |
| 9 | 9 | 2021 | 10 | 234 | 2327 |
| 10 | 10 | 2021 | 11 | 272 | 2599 |
| 11 | 11 | 2021 | 12 | 358 | 2957 |
绘制图形:
1 | # 设置画布大小 |
Out:

1 | ## 存储新数据 |



